Binomische Formeln

3.Klasse (Österreichischer Schulplan)

Was sind Binomische Formeln:
Als binomische Formel bezeichnet man ein Binom, das quadriert oder noch höher potenziert wird, zum Beispiel $ (x+y)^2 $ ist eine binomische Formel, $x^2$ aber nicht. Wir sehen auch dass mindestens zwei Summanden in der Klammer stehen müssen (die voneinander addiert / subtrahiert werden), ein Buchstabe genügt nicht, wie wir oben gesehen haben, das ist ein normal potenzierter Term, der andere aber eine binomische Formel!

Wenn mehr als zwei Summanden / Differenzen in der Klammer stehen, ist es auch eine binomische Formel, z.B. $ (a+b+c)^2 $

1.Binomische Formel:
$ (a+b)^2=a^2+2ab+b^2 $

Herleitung rechnerisch:
$ \underline{\underline{ (a+b)^2 }} = (a+b) \cdot (a+b) = a^2 +ab+ba+b^2 = \underline{\underline{ a^2+2ab+b^2 }} $

Herleitung graphisch:

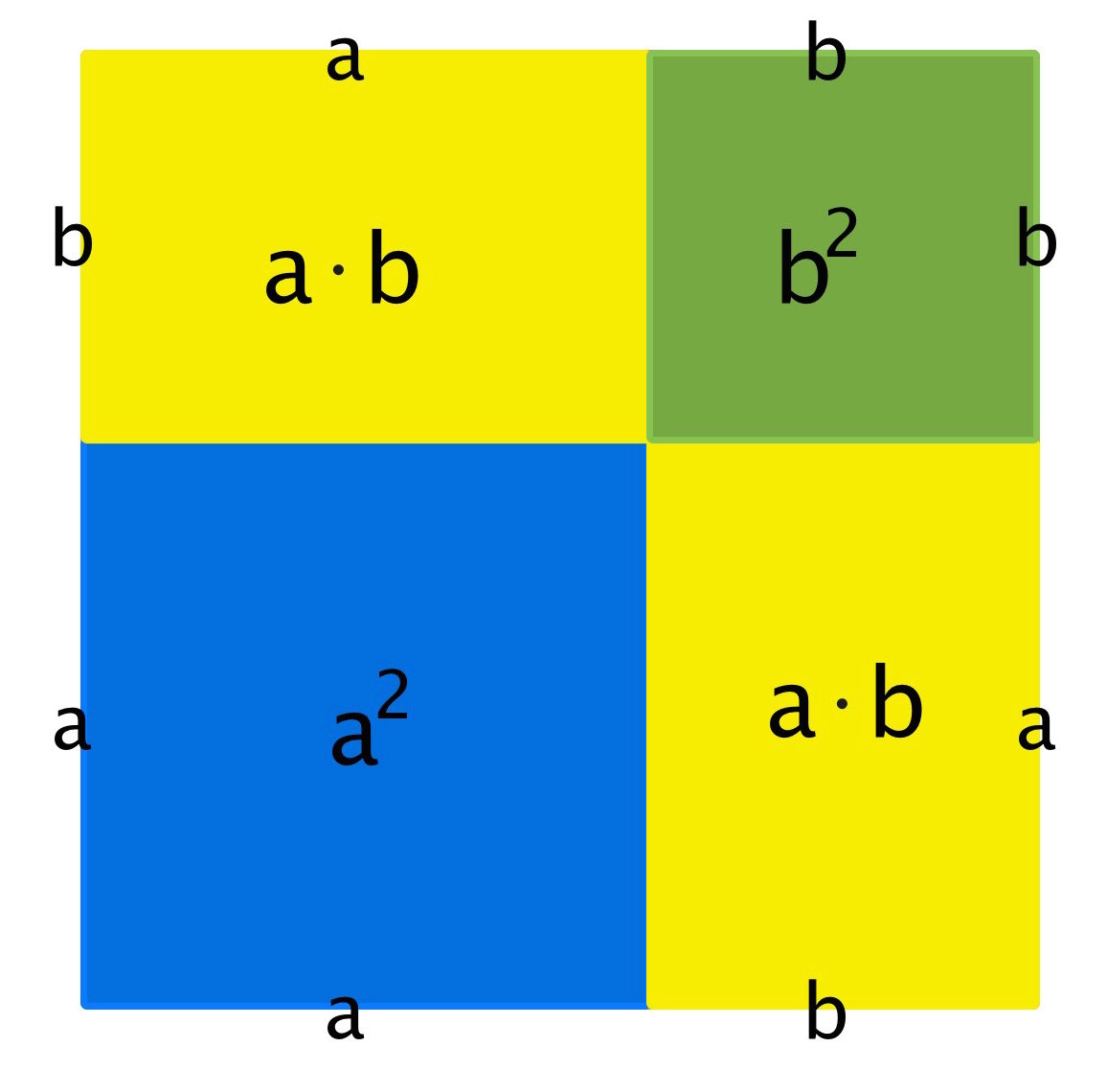
Der Flächeninhalt des blauen Quadrats ist $a^2$, der Flächeninhalt des grünen Quadrats ist $b^2$ und der Flächeninhalt der gelben Rechtecke ist $2 \cdot a \cdot b$ . Die Summe der ganzen Flächeninhalte ist der Flächeninhalt des ganzen Quadrats. Also der Flächeninhalt des Quadrats ist $a^2+b^2+2ab$.

Der Flächeninhalt des Quadrats kann aber auch so berechnet werden. Die Seitenlänge des Quadrats ist $(a+b)$, der Flächeninhalt also: $(a+b)^2$. Also gilt, dass $(a+b)^2 = a^2+2ab+b^2$ ist.

2.Binomische Formel:
$ (a-b)^2=a^2-2ab+b^2 $

Herleitung rechnerisch:
$ \underline{\underline{ (a-b)^2 }} = (a-b) \cdot (a-b) = a^2 -ab-ba+b^2 = \underline{\underline{ a^2-2ab+b^2 }} $

3.Binomische Formel:
$ (a+b) \cdot (a-b)=a^2-b^2 $

Herleitung rechnerisch:
$ \underline{\underline{ (a+b) \cdot (a-b) }} = a^2 -ab+ba-b^2 = \underline{\underline{ a^2-b^2 }} $

Beispiele:
$ (2x+3y)^2 $ (in diesem Beispiel ist $a=2x$ und $b=3y$)
Also: $(2x)^2+2\cdot2x\cdot3y+(3y)^2 = 4x^2+12xy+9y^2$

$ (3a+4b)^2 $ (in diesem Beispiel ist $ a=3a$ und $b=4b$)
Also: $(3a)^2+2\cdot3a\cdot4b+(4b)^2=9a^2+24ab+16b^2$

$ (4u-6v)^2 $ (in diesem Beispiel ist $ a=4u$ und $b=6v$)
Also: $(4u)^2-2\cdot4u\cdot6v+(6v)^2=16u^2-48uv+36v^2$

$ (2w-3r)^2 $ (in diesem Beispiel ist $ a=2w$ und $b=3r$)
Also: $(2w)^2-2\cdot2w\cdot3r+(3r)^2=4w^2-12wr+9r^2$

$ (4x+5y)\cdot(4x-5y) $ (in diesem Beispiel ist $ a=4x$ und $b=5y$)
Also: $4x\cdot4x-5y\cdot5y=16x^2-25y^2$

$ (3x+7y)\cdot(3x-7y) $ (in diesem Beispiel ist $ a=3x$ und $b=7y$)
Also: $3x\cdot3x-7y\cdot7y=9x^2-49y^2$

Weitere Binomische Formeln (Exkurs):

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a-b)^3=a^3-3a^2b+3ab^2-b^3$
$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Über die Autoren dieser Seite

Unsere Seiten werden von einem Team aus Experten erstellt, gepflegt sowie verwaltet. Wir sind alle Mathematiker und Lehrer mit abgeschlossenem Studium und wissen, worauf es bei mathematischen Erklärungen ankommt. Deshalb erstellen wir Infoseiten, programmieren Rechner und erstellen interaktive Beispiele, damit dir Mathematik noch begreifbarer gemacht werden kann. Dich interessiert unser Projekt? Dann melde dich bei admin@mathespass.at!